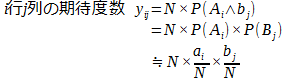独立性検定とは、クロス集計表を作成したとき、2つの属性が独立であるかどうかを統計的に判定する方法です。
独立性検定を行う手順は次の通りです。
独立性検定を行う手順は次の通りです。
- 仮説を立てる
- 帰無仮説H0:属性Ai(i=1,…,m)とBj(j=1,…,n)は独立である
- 対立仮説H1:属性Ai(i=1,…,m)とBj(j=1,…,n)は少なくとも一つ以上は独立でない
-
B1 B2 ・・・ Bn 合計 A1 x11 x12 ・・・ x1n a1 A2 x21 x22 ・・・ x2n a2 ・・・ ・・・ ・・・ ・・・ ・・・ ・・・ Am xm1 xm2 ・・・ xmn am 合計 b1 b2 ・・・ bn N - AiとBjの期待度数yijを次の式により求めます
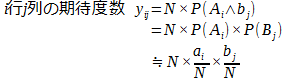
- 検定統計量Tを次のように計算します

- このとき、検定統計量Tは自由度(m-1)(n-1)のカイ二乗分布に従うので、有意水準のカイ二乗値kと比較します
- T>kであれば、帰無仮説を棄却して、対立仮説を採用します
例
男女200人に朝食・昼食・夕食について、どの時間帯の食事を最も重要視するかの調査を行った結果、次の表になりました。このとき、男女と朝食・昼食・夕食について独立であるかどうかを調べます。
| 朝食 | 昼食 | 夕食 | 合計 | |
|---|---|---|---|---|
| 男 | 50 | 15 | 55 | 120 |
| 女 | 10 | 40 | 30 | 80 |
| 合計 | 60 | 55 | 85 | 200 |
- 帰無仮説H0:男女と朝食・昼食・夕食は独立である
期待度数の計算式は次のようになります。
| 朝食 | 昼食 | 夕食 | 合計 | |
|---|---|---|---|---|
| 男 | 200×(120/200)×(60/200) | 200×(120/200)×(55/200) | 200×(120/200)×(85/200) | 120 |
| 女 | 200×(80/200)×(60/200) | 200×(80/200)×(55/200) | 200×(80/200)×(85/200) | 80 |
| 合計 | 60 | 55 | 85 | 200 |
期待度数の値は次のようになります。
| 朝食 | 昼食 | 夕食 | 合計 | |
|---|---|---|---|---|
| 男 | 36 | 33 | 51 | 120 |
| 女 | 24 | 22 | 34 | 80 |
| 合計 | 60 | 55 | 85 | 200 |
検定統計量は次のようになります。
| 朝食 | 昼食 | 夕食 | 合計 | |
|---|---|---|---|---|
| 男 | (50-36)2/36 | (15-33)2/33 | (55-51)2/51 | |
| 女 | (10-24)2/24 | (40-22)2/22 | (30-34)2/34 | |
| 合計 |
| 朝食 | 昼食 | 夕食 | 合計 | |
|---|---|---|---|---|
| 男 | 5.4444 | 9.8181 | 0.3137 | 15.5762 |
| 女 | 8.1666 | 14.7272 | 0.4705 | 23.3643 |
| 合計 | 13.611 | 24.5453 | 0.7842 | 38.9405 |
これから検定統計量はT=38.9405となります。
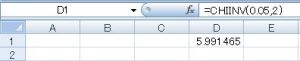
これは、自由度(2-1)(3-1)=2のカイ二乗分布に従うので、有意水準を0.05とすると、カイ二乗値は5.991465となります。
エクセルでこの値を求めるときは、CHIINV関数を使います。
CHIINV(確率,自由度)
今回の例では、セルに「=CHIINV(0.05,2)」を入力します。
T=38.9405>5.991465から棄却域に入るので、帰無仮説H0は棄却されます。よって、男女と朝食・昼食・夕食は少なくとも一つ以上は独立でないとされます。
Rで計算する
Rで独立性検定を行う場合は、次のようになります。
chisq.test(matrix(c(50, 15, 55, 10, 40, 30), ncol=3, byrow=T))
Pearson's Chi-squared test
data: matrix(c(50, 15, 55, 10, 40, 30), ncol = 3, byrow = T)
X-squared = 38.9409, df = 2, p-value = 3.5e-09
よって、有意水準を5%(=0.05)とすると、p-value=3.5e-09<0.05となるため、帰無仮説は棄却されます。
Pythonで計算する
Pythonで独立性検定を行う場合は、次のようになります。あらかじめ、numpyとscipyパッケージをインストールしておきます。
import numpy as np
from scipy import stats
print(stats.chi2_contingency(np.array([[50, 15, 55], [10, 40, 30]]))
これを実行すると、次のように表示される。
(38.940879382055854, 3.5002211279659769e-09, 2, array([[36., 33., 51.], [24., 22., 34.]]))
これは、次のような意味である。
- 検定統計量:38.940879382055854
- p値:3.5002211279659769e-09
- 自由度:2
- 期待度数:array([[36., 33., 51.], [24., 22., 34.]])