R検定 カイ二乗検定 – 適合度検定

適合度検定とは、観測度数分布が期待度数分布と同じかどうかを統計的に確かめる方法です。
適合度検定を行う手順は次の通りです。

1. 仮説を立てる
   • 帰無仮説 H₀：観測度数分布と期待度数分布が同じ
   • 対立仮説 H₁：観測度数分布と期待度数分布が同じではない

2. 	A1	A2	・・・	An	合計
   観測度数	x1	x2	・・・	xn	X
   期待度数	y1	y2	・・・	yn	Y

3. 期待度数y_i{i=1,..,n}が5以下の場合は、隣接する列と合わせる
4. 検定統計量Tを次のように計算する。
   
5. このとき、検定統計量Tは自由度(n-1)のカイ二乗分布に従うので、有意水準のカイ二乗値kと比較する。
6. T>kであれば、帰無仮説を棄却して、対立仮説を採用する。

例

日本人のABO式血液型の分布は大まかにA型が40%、B型が20%、O型が30%、AB型が10%とされています（「ABO式血液型 – Wikipedia」より）。
100人に血液型を調査したとき、A型が47人、B型が18人、O型が27人、AB型が8人であった場合、日本人のABO式血液型の分布に従っているかを確認してみます。
そこで、帰無仮説は次のようになります。

• 帰無仮説 H₀：A型が40%、B型が20%、O型が30%、AB型が10%である

期待度数は観測度数合計×割合となるので、まとめると次のようになります。

血液型	A型	B型	O型	AB型	合計
観測度数	47	18	27	8	100
割合	0.4	0.2	0.3	0.1	1
期待度数（＝観測度数合計×割合）	40	20	30	10	100

次にそれぞれに対して、(観測度数 – 期待度数)²/期待度数を求めます。

血液型	A型	B型	O型	AB型	合計
(観測度数-期待度数)2/期待度数	(47-40)2/40	(18-20)2/20	(27-30)2/30	(8-10)2/10
(観測度数-期待度数)2/期待度数	1.225	0.200	0.300	0.400	2.125

これから検定統計量はT=2.125となります。
これは、自由度(4-1)=3のカイ二乗分布に従うので、有意水準を0.05とするとカイ二乗値は7.81473となります。
エクセルでこの値を求めるときは、CHIINV関数を使います。

CHIINV(確率,自由度)

今回の例では、セルに「=CHIINV(0.05,3)」を入力します。

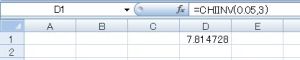
T=2.125<7.81473から棄却域に入らないので帰無仮説H₀を棄却できない。
よって、調査結果は統計的にA型が40%、B型が20%、O型が30%、AB型が10%であるといえます。

Rで計算する

Rで適合度検定を行う場合は、次のようになります。

chisq.test(c(47, 18, 27, 8), p = c(0.4, 0.2, 0.3, 0.1))

    Chi-squared test for given probabilities

    data:  c(47, 18, 27, 8)
    X-squared = 2.125, df = 3, p-value = 0.5469

よって、有意水準を5%(=0.05)とすると、p-value=0.5469>0.05となるため、帰無仮説は棄却されません。

Pythonで計算する

Pythonで適度度検定を行う場合は、次のようになります。あらかじめ、scipyパッケージをインストールしておきます。

from scipy import stats
result = stats.chisquare([47, 18, 27, 8], f_exp = [40, 20, 30, 10])
print(result)

これを実行すると、次のようになる。

(2.125, 0.5468716738890154)

これは、カイ二乗値2.125、p値0.5468という意味である。