R×rpart 決定木 – 回帰木 | トライフィールズ

ここでは、決定木の目的変数が連続値である場合の回帰木について、R言語の「rpart」パッケージを用いて簡単に見ていきます。
まずは必要となるパッケージのインストールとロードを行います。「rpart」パッケージは決定木を行うためのものだが、「rpart.plot」と「partykit」パッケージは結果を視覚的に表示するために使うので、あらかじめインストールとロードをしておきます。


install.packages("rpart")
install.packages("rpart.plot")
install.packages("partykit")
library(rpart)
library(rpart.plot)
library(partykit)

サンプルデータとして、「rpart」パッケージに含まれる「cu.summary」を使いました。


head(cu.summary)
                Price Country Reliability Mileage  Type
Acura Integra 4 11950   Japan Much better      NA Small
Dodge Colt 4     6851   Japan              NA Small
Dodge Omni 4     6995     USA  Much worse      NA Small
Eagle Summit 4   8895     USA      better      33 Small
Ford Escort   4  7402     USA       worse      33 Small
Ford Festiva 4   6319   Korea      better      37 Small

決定木を実行するには、rpart関数を用います。目的変数が連続値であれば、自動的に回帰木として扱われます。同様に、目的変数がカテゴリ値ならば分類木として扱われます。


rt <- rpart(Price ~ Mileage + Type + Country, data = cu.summary)
print(rt)
n= 117 

node), split, n, deviance, yval
      * denotes terminal node

   1) root 117 7407473000 15743.460  
     2) Type=Compact,Small,Sporty,Van 80 3322389000 13035.010  
       4) Country=Brazil,France,Japan,Japan/USA,Korea,Mexico,USA 69 1426421000 11555.160  
         8) Type=Small 21   50309830  7629.048 *
         9) Type=Compact,Sporty,Van 48  910790000 13272.830  
           18) Country=Japan/USA,Mexico,USA 29  482343500 12241.550 *
           19) Country=France,Japan 19  350528000 14846.890 *
       5) Country=Germany,Sweden 11  797004200 22317.730 *
     3) Type=Large,Medium 37 2229351000 21599.570  
       6) Country=France,Korea,USA 25 1021102000 18697.280  
         12) Type=Medium 18  741101600 17607.440 *
	     13) Type=Large 7  203645100 21499.710 *
       7) Country=England,Germany,Japan,Sweden 12  558955000 27646.000 *

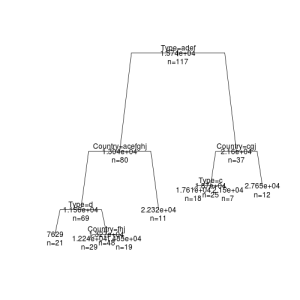
この結果をもっと視覚的に分かりやすいグラフとして表示してみます。まずは、標準のplot関数を用いてみます。


par(xpd = NA)
plot(rt, branch = 0.8, margin = 0.05)
text(rt, use.n = TRUE, all = TRUE)

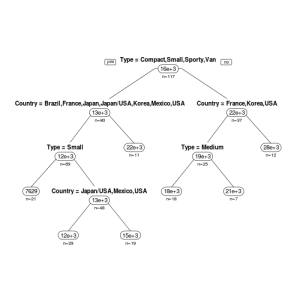
次に、「rpart.plot」パッケージのrpart.plot関数を用いてみます。


rpart.plot(rt, type = 1, uniform = TRUE, extra = 1, under = 1, faclen = 0)

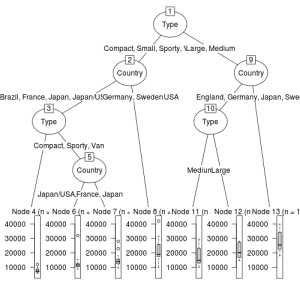
最後に、「partykit」パッケージのas.party関数用いてデータを変換したものをplot関数に用いてみます。


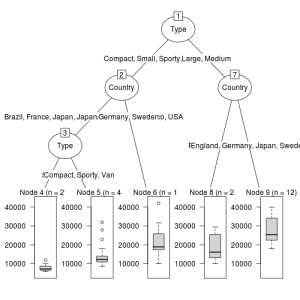
plot(as.party(rt))

これらのグラフはそれぞれ見栄えが異なるので、気に入ったものを使えばよいと思うが、「partkit」パッケージを用いたものが、比較的誰にでもわかりやすいように感じた。
次に剪定を考えるため、printcp関数と、plotcp関数を実行してみます。


printcp(rt)

Regression tree:
rpart(formula = Price ~ Mileage + Type + Country, data = cu.summary)

Variables actually used in tree construction:
[1] Country Type   

Root node error: 7407472615/117 = 63311732

n= 117 

        CP nsplit rel error  xerror    xstd
1 0.250522      0   1.00000 1.01365 0.15804
2 0.148359      1   0.74948 0.90282 0.16685
3 0.087654      2   0.60112 0.79992 0.15733
4 0.062818      3   0.51347 0.65730 0.11368
5 0.010519      4   0.45065 0.55595 0.10363
6 0.010308      5   0.44013 0.57370 0.10665
7 0.010000      6   0.42982 0.57370 0.10665

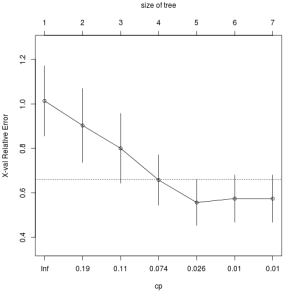
plotcp(rt)

plotcp関数の結果から剪定の基準をcp=0.026として、再度決定木を行うと以下のようになります。


rt2 <- rpart(Price ~ Mileage + Type + Country, data = cu.summary, cp = 0.026)
print(rt2)
n= 117 

node), split, n, deviance, yval
      * denotes terminal node

  1) root 117 7407473000 15743.460  
    2) Type=Compact,Small,Sporty,Van 80 3322389000 13035.010  
      4) Country=Brazil,France,Japan,Japan/USA,Korea,Mexico,USA 69 1426421000 11555.160  
        8) Type=Small 21   50309830  7629.048 *
        9) Type=Compact,Sporty,Van 48  910790000 13272.830 *
      5) Country=Germany,Sweden 11  797004200 22317.730 *
    3) Type=Large,Medium 37 2229351000 21599.570  
      6) Country=France,Korea,USA 25 1021102000 18697.280 *
      7) Country=England,Germany,Japan,Sweden 12  558955000 27646.000 *

predict関数を用いると、予測が可能となります。ここでは、簡単のため、cu.summaryデータを二分割したものを用います。


train <- cu.summary[1:100,]
test <- cu.summary[101:112,]
rtp <- rpart(Price ~ Mileage + Type + Country, data = train)
p <- predict(rtp, newdata = test)
print(p)
          Buick Electra V6          Buick Le Sabre V6 
                  11981.79                   11981.79 
      Cadillac Brougham V8       Cadillac De Ville V8 
                  11981.79                   11981.79 
      Chevrolet Caprice V8 Ford LTD Crown Victoria V8 
                  11981.79                   11981.79 
       Lincoln Town Car V8         Chevrolet Astro V6 
                  11981.79                   11981.79 
   Chevrolet Lumina APV V6            Dodge Caravan 4 
                  11981.79                   11981.79 
    Dodge Grand Caravan V6           Ford Aerostar V6 
                  11981.79                   11981.79

R×rpart 決定木 – 回帰木