R×rpart 決定木 – 分類木

決定木とは、分類ルールを木構造で表したものです。分類したいデータを目的変数（従属変数）、分類するために用いるデータを説明変数（独立変数）といいます。目的変数がカテゴリデータなどの場合は「分類木」、連続値などの量的データの場合は「回帰木」と呼ばれます。
決定木の最大のメリットは、結果にグラフを用いることができるため、視覚的に確認できることです。
ここでは、R言語の「rpart」パッケージを用いて決定木について見ていきます。サンプルデータとして、Rに標準で含まれている「Titanic」を使います。このサンプルデータはタイタニック号の乗客の属性情報と生死の情報が含まれています。生死を分けた要因を属性情報から分類するとどのようになるのかを見ていきます。
まずは必要となるパッケージのインストールとロードを行います。「rpart」パッケージは決定木を行うためのものだが、「rpart.plot」と「partykit」パッケージは結果を視覚的に表示するために使うので、あらかじめインストールとロードをしておきます。

install.packages("rpart")
install.packages("rpart.plot")
install.packages("partykit")
library(rpart)
library(rpart.plot)
library(partykit)

次に、サンプルデータを扱いやすい形に変更しておきます。

tmp <- data.frame(Titanic)
df <- data.frame(
(con)      Class = rep(tmp$Class, tmp$Freq),
(con)      Sex = rep(tmp$Sex, tmp$Freq),
(con)      Age = rep(tmp$Age, tmp$Freq),
(con)      Survived = rep(tmp$Survived, tmp$Freq)
(con)  )
head(df)
  Class  Sex   Age Survived
1   3rd Male Child       No
2   3rd Male Child       No
3   3rd Male Child       No
4   3rd Male Child       No
5   3rd Male Child       No
6   3rd Male Child       No

決定木を実行するにはrpart関数を用います。下の意味は、Survivedを目的変数、ClassとSexとAgeを説明変数として分類木を用いて、結果をctに格納しています。そして結果をprint関数で表示しています。

ct <- rpart(Survived ~ Class + Sex + Age, data = df, method = "class")
print(ct)
n= 2201 

node), split, n, loss, yval, (yprob)
  * denotes terminal node

   1) root 2201 711 No (0.6769650 0.3230350)  
     2) Sex=Male 1731 367 No (0.7879838 0.2120162)  
       4) Age=Adult 1667 338 No (0.7972406 0.2027594) *
       5) Age=Child 64  29 No (0.5468750 0.4531250)  
        10) Class=3rd 48  13 No (0.7291667 0.2708333) *
        11) Class=1st,2nd 16   0 Yes (0.0000000 1.0000000) *
     3) Sex=Female 470 126 Yes (0.2680851 0.7319149)  
       6) Class=3rd 196  90 No (0.5408163 0.4591837) *
       7) Class=1st,2nd,Crew 274  20 Yes (0.0729927 0.9270073) *

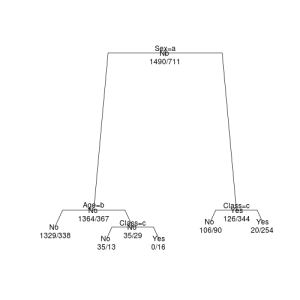
この結果をもっと視覚的に分かりやすいグラフとして表示してみます。まずは、標準のplot関数を用いてみます。

par(xpd = NA)
plot(ct, branch = 0.8, margin = 0.05)
text(ct, use.n = TRUE, all = TRUE)

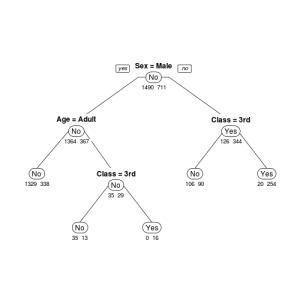
次に、「rpart.plot」パッケージのrpart.plot関数を用いてみます。

rpart.plot(ct, type = 1, uniform = TRUE, extra = 1, under = 1, faclen = 0)

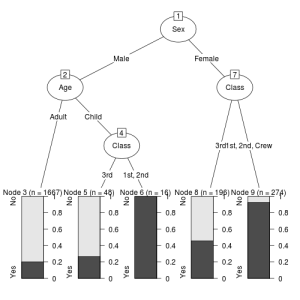
最後に、「partykit」パッケージのas.party関数用いてデータを変換したものをplot関数に用いてみます。

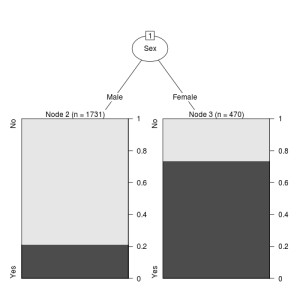
plot(as.party(ct))

これらのグラフはそれぞれ見栄えが異なるので、気に入ったものを使えばよいと思うが、「partkit」パッケージを用いたものが、比較的誰にでもわかりやすいように感じました。
さて、このグラフからまず分かることは、生死を決定づけた主な要因は性別（Sex）であることが分かります。大人であれ子供であれ、良い部屋に泊まっていようとなかろうと、女性（Female）の乗客は生存率が高くなっています。
また、男性（Male）であっても、子供（Child）で良い部屋に泊まっていた乗客の生存率は高くなっています。
つまり、この決定木からはタイタニック号が今まさに沈没しようとしているとき、真っ先に女性や子供を優先的に避難させようとしたことが読み取れます。
このように、決定木を用いると、視覚的に様々なものが読み取れるため非常に便利であるが、データによっては、木構造が深く複雑になる場合があります。そのようなときに、あまり重要でない分類ルールを失くしてシンプルにする必要があります。このような方法は剪定と呼ばれます。
剪定とは、構築された木が深くなるほど、きちんと分類できているといえるが、過学習の可能性もあります。そこで、あらかじめ定めたパラメータによって複雑さと制御する方法です。
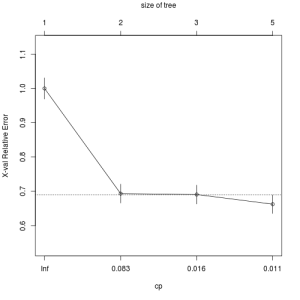
どのように剪定を行うのが良いかを判断するためには「rpart」パッケージのprintcp関数とグラフで表示できるplotcp関数を用います。printcp関数は、分岐の数と複雑度を対応させて、plotcp関数は木のサイズと対応させています。どちらを用いてもよいが、基本的には、errorが収束し始めているところを剪定の基準にする場合が多いです。

printcp(ct)

Classification tree:
rpart(formula = Survived ~ Class + Sex + Age, data = df, method = "class")

Variables actually used in tree construction:
[1] Age   Class Sex  

Root node error: 711/2201 = 0.32303

n= 2201 

        CP nsplit rel error  xerror     xstd
1 0.306610      0   1.00000 1.00000 0.030857
2 0.022504      1   0.69339 0.69339 0.027510
3 0.011252      2   0.67089 0.69058 0.027470
4 0.010000      4   0.64838 0.66245 0.027062

plotcp(ct)

printcp関数の結果から剪定の基準をcp=0.022504として、再度決定木を行うと以下のようになります。

ct2 <- rpart(Survived ~ Class + Sex + Age, data = df, method = "class", cp = 0.022504)
print(ct2)
n= 2201 

node), split, n, loss, yval, (yprob)
      * denotes terminal node

  1) root 2201 711 No (0.6769650 0.3230350)  
    2) Sex=Male 1731 367 No (0.7879838 0.2120162) *
    3) Sex=Female 470 126 Yes (0.2680851 0.7319149) *

plot(as.party(ct2))

predict関数を用いると、予測が可能となります。ここでは、簡単のため、Titanicデータを二分割したものを用います。
以下を見ると、2001番目のデータは生存した（Yes）確率が高いということが分かります。

train <- df[1 : 2000,]

test <- df[2001 : 2201,]

ctp <- rpart(Survived ~ Class + Sex + Age, data = train, method = "class")

p <- predict(ctp, newdata = test)

head(p)

             No       Yes

2001 0.03333333 0.9666667

2002 0.03333333 0.9666667

2003 0.03333333 0.9666667

2004 0.03333333 0.9666667

2005 0.03333333 0.9666667

2006 0.03333333 0.9666667