平均値 (mean)
平均値は、データの値をすべて足して、その個数で割った数値です。例えば、データの集合{1,2,3,4,5}ならば平均値3です。注意していただきたいのは、データの集合の中に極端に他の値と異なる値があった場合です。例えば、データ集合{1,2,3,4,5,100000}の平均値は果たしてデータを代表しているといえるでしょうか。平均値には、必ずこのような問題が付きまとうので、ヒストグラムなどでデータの分布を確認するのが望ましいです。平均値を計算するサンプルコードは次になります。
x <- iris$Sepal.Length
mean(x)
[1] 5.843333
中央値 (median)
中央値は、データを昇順で並び替えたときの真ん中の値のことです。データの個数が奇数のときは、ちょうど真ん中の数値であり、データの個数が偶数のときは、真ん中の2つの数値の平均値となります。
もう少し正確に記載すると、n個の数値データの集合を x1≦x2≦…≦xn と並び替えたとき、次の値が中央値となります。
- nが偶数 (even) の場合:
- nが奇数 (odd) の場合:
例えば、データの集合{1,2,3,4,5}ならば中央値3、データの集合{1,2,3,4}ならば中央値2.5となります。中央値を計算するサンプルコードは次になります。
x <- iris$Sepal.Length
median(x)
[1] 5.8
最頻値 (mode)
最頻値とは、データの集合の中で、最も頻繁に現れる値のことです。例えば、データの集合{1,2,2,3,4,5}ならば最頻値2となります。
ただし、一般に数値データの集合の場合、同じ数値が頻繁に現れることは少ないです。このときは、数値データの度数分布表を作成し、最も度数が高い階級の階級値を最頻値とします。度数分布表の階級の取り方により、最頻値が変わってしまうことに注意してください。最頻値を計算するサンプルコードは次になります。
x <- iris$Sepal.Length
names(which.max(table(x)))
[1] "5"
最大値 (maximum)
最大値とは、データの集合の中で、最も大きい値のことです。例えば、データの集合{1,2,3,4,5}ならば最大値5となります。最大値を計算するサンプルコードは次になります。
x <- iris$Sepal.Length
max(x)
[1] 7.9
最小値 (minimum)
最小値とは、データの集合の中で、最も小さい値のことです。例えば、データの集合{1,2,3,4,5}ならば最小値1となります。最小値を計算するサンプルコードは次になります。
x <- iris$Sepal.Length
min(x)
[1] 4.3
分散 (variance)
平均値からの散らばり具合を表す代表値を分散といいます。
分散は2種類あり、母集団での(推定された)分散を不偏分散といい、標本(サンプル)そのものの分散を標本分散といいます。
不偏分散 (unbiased variance)
不偏分散は、データが得られたときの対象としている母集団に対する分散となります。
不偏分散は次で定義されます。ただし、は得られたデータの平均値です。
不偏分散を計算するサンプルコードは次になります。
x <- iris$Sepal.Length
var(x)
[1] 0.6856935
標本分散 (sample variance)
標本分散は、データが得られたときの標本(サンプル)に対する分散となります。
標本分散は次で定義されます。ただし、は得られたデータの平均値です。
標本分散を計算するサンプルコードは次になります。
x <- iris$Sepal.Length
((length(x) - 1) / length(x) ) * var(x)
[1] 0.6811222
標準偏差 (standard deviation)
標準偏差とは、分散の正の平方根の値のことです。
なぜわざわざ分散の正の平方根を標準偏差と改めて名前をつけているのかについて、簡単に説明します。
例えば、花びらのがく片の長さの集団を考えます。
このとき、分散の式を見ると、2乗した値となっていることから、分散の単位は「長さ×長さ」となっています。標準偏差は、この分散の平方根を取ることにより、単位を「長さ」に戻しているとみることができます。
平均値などは単位が変わらないのに、分散を考えると単位が変わってしまうのでは扱い難いとうわけです。そこで、同じ単位の枠内で扱えるように分散を変更したのが標準偏差であるといえます。
不偏標準偏差 (unbiased standard deviation)
不偏標準偏差は、不偏分散の平方のことです。不偏標準偏差を計算するサンプルコードは次になります。
x <- iris$Sepal.Length
sd(x)
[1] 0.8280661
標本標準偏差 (sample standard deviation)
標本標準偏差は、標本分散の平方のことです。標本標準偏差を計算するサンプルコードは次になります。
x <- iris$Sepal.Length
sqrt((length(x) - 1) / length(x) ) * sd(x)
[1] 0.8253013
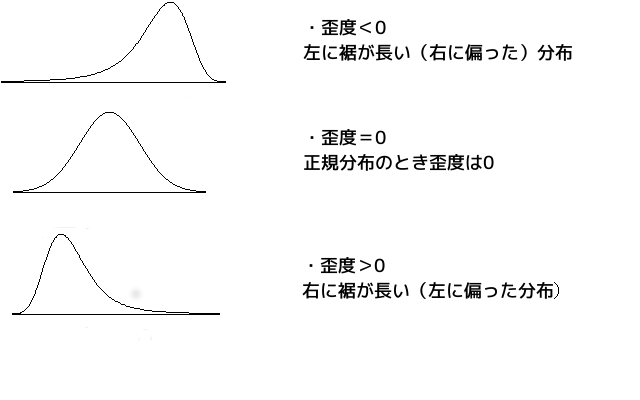
歪度 (わいど, skewness)
歪度とは、分布の非対称性を表す値のことである。
- 歪度<0:左に裾が長い(右に偏った)分布
- 歪度=0:正規分布と同じ
- 歪度>0:右に裾が長い(左に偏った)分布
x <- iris$Sepal.Length
mean((x-mean(x))^3)/(sd(x)^3)
[1] 0.3086407
尖度 (せんど, kurtosis)
尖度とは、分布の尖り度合いを表す値のことである。
- 尖度<3:なだらかな分布
- 尖度=0:正規分布のときは尖度は3
- 尖度>3:尖っている分布
尖度を計算するサンプルコードは次になります。
x <- iris$Sepal.Length
> x mean((x-mean(x))^4)/(sd(x)^4)
[1] 2.394187