Pythonで与えられた度数分布に従う乱数を生成する方法をご紹介する。
さっそくだが、全コードを以下に記す。
さっそくだが、全コードを以下に記す。
import random
import matplotlib.pyplot as plt
def random_freq_index(freq_list):
""" 度数分布表から乱数を生成してインデックス番号を返します
Args:
freq_list:度数リスト
Returns:
リストのインデックス
"""
total = sum(x for x in freq_list)
cum_freq = 0
dis = [cum_freq]
for x in freq_list:
cum_freq += x
dis.append(float(cum_freq) / total)
r = random.random()
i = 0
while dis[i] < r:
i += 1
return i - 1
def random_freq(freq_list):
""" 度数分布表から乱数を生成して[0,1)の数値を返します
Args:
freq_list:度数リスト
Returns:
[0,1)の数値
"""
total = sum(x for x in freq_list)
cum_freq = 0
dis = [cum_freq]
for x in freq_list:
cum_freq += x
dis.append(float(cum_freq) / total)
r = random.random()
i = 0
while dis[i] < r:
i += 1
x0 = 1.0 / len(freq_list)
return ((r - dis[i - 1]) / (dis[i] - dis[i - 1])) * x0 + (i - 1) * x0
if __name__ == '__main__' :
indexes = []
values = []
for i in range(1000):
indexes.append(random_freq_index([20, 50, 25, 10, 100]))
values.append(random_freq([20, 50, 25, 10, 100]))
agg = [0,0,0,0,0]
for i in indexes:
agg[i] += 1
print(agg)
plt.hist(values)
plt.show()
これを適当な名前を付けてファイルに保存して実行すると、
[99, 254, 139, 50, 458]
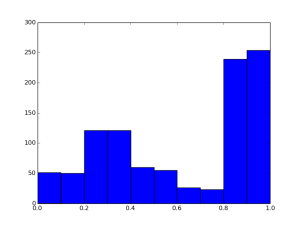
となり大体[20,50,25,10,100]の割合となっていることが分かる。また、表示されるヒストグラムは以下のようになる。