R K-means法のクラスタ数を機械的に決定する方法

K-means法（Ｋ平均法）を用いてクラスタリングする場合は、あらかじめクラスタ数を指定しなければならない。
このときのクラスタ数をどのように決めてよいか迷ったことはないだろうか。
ここでは、K-means法のクラスタ数を機械的に決定する方法をお伝えする。

K-means法のクラスタ数を機械的に決定するために用いるのが、Gap統計量である。
Gap統計量を用いたクラスタ数の決定のアイディアを簡単にご紹介すると、クラスタ数1、2、・・・と順に、一様分布から作成されたクラスタ内の距離の平均と元データのクラスタ内の距離の平均とを比べて、より密集しているクラスタ数を採用するという方法である。

詳しくは、Estimating the number of clusters in a data set via the gap statisticを参考にしてほしい。

ここからは、Rを用いて具体的に見ていこう。
まずは、clusterパッケージの読み込みと、ご説明するためのサンプルデータを作成する。
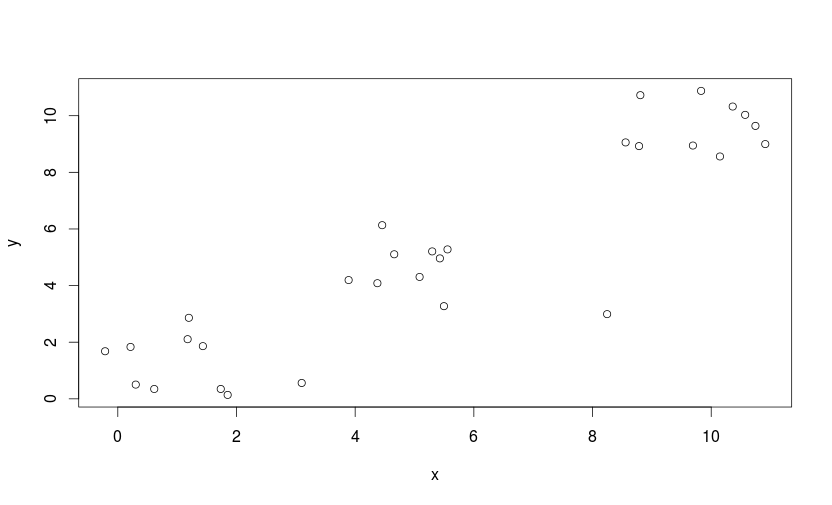
意図的に3つのクラスタができるようにデータを作成した。

> library(cluster)

> sample1 <- data.frame(x = rnorm(10, mean = 1, sd = 1), y = rnorm(10, mean = 1, sd = 1))
> sample2 <- data.frame(x = rnorm(10, mean = 5, sd = 1), y = rnorm(10, mean = 5, sd = 1))
> sample3 <- data.frame(x = rnorm(10, mean = 10, sd = 1), y = rnorm(10, mean = 10, sd = 1))
> sample <- rbind(sample1, sample2, sample3)
> plot(sample)

このデータに対して、Gap統計量を求めてみる。
Gap統計量を求めるためには、clusGap関数を用いる。
下のコードのclusGap関数の引数は、次のような意味である。

• sample：データ
• kmenas：K-means法
• K.max：クラスタ数の最大値
• B：モンテカルロ法のブートストラップ回数
• verborse：処理状況を表示するかどうか

> result <- clusGap(sample, kmeans, K.max = 10, B = 100, verbose = interactive())

Clustering k = 1,2,..., K.max (= 10): .. done
Bootstrapping, b = 1,2,..., B (= 100)  [one "." per sample]:
.................................................. 50 
.................................................. 100 

処理が終わったら、結果の中身を見てみよう。

> result

Clustering Gap statistic ["clusGap"].
B=100 simulated reference sets, k = 1..10
 --> Number of clusters (method 'firstSEmax', SE.factor=1): 3
          logW   E.logW         gap     SE.sim
 [1,] 3.806407 3.629772 -0.17663555 0.06747599
 [2,] 3.062174 3.097019  0.03484477 0.06139314
 [3,] 2.453365 2.839130  0.38576490 0.07033063
 [4,] 2.327831 2.655896  0.32806576 0.07766857
 [5,] 2.209761 2.491554  0.28179274 0.09399472
 [6,] 2.107407 2.336471  0.22906381 0.09037798
 [7,] 1.998367 2.196959  0.19859206 0.09656801
 [8,] 1.778149 2.071716  0.29356688 0.11532498
 [9,] 1.681060 1.943485  0.26242534 0.10098396
[10,] 1.658722 1.821823  0.16310132 0.10548041

このとき、求めるクラスタ数kは

gap(k) ≧ gap(k+1) - SE.sim(k+1)

となる最小のkである。

clusGap関数の結果をみると、k=3であることが分かる。
このclusGap関数は、グラフ化することも容易で、グラフから読み解くこともできる。

> plot(result)

このグラフから、求めるクラスタ数はk=3であることが分かる。