相関係数とは2変量のデータ間の関係性の強弱を計る統計学的指標です。相関係数rがとる値の範囲は-1≦r≦1となります。相関係数rの値により以下のように呼ばれます。
- -1≦r<0ならば負の相関
- r=0ならば無相関
- 0<r≦1ならば正の相関
一般的に、強弱も合わせて以下のように呼ばれます。
| -1≦r<-0.7 | 強い負の相関がある |
| -0.7≦r<-0.4 | かなり負の相関がある |
| -0.4≦r<-0.2 | やや負の相関がある |
| -0.2≦r<0 | ほとんど負の相関がない |
| r=0 | 相関がない |
| 0<r≦0.2 | ほとんど正の相関がない |
| 0.2<r≦0.4 | やや正の相関がある |
| 0.4<r≦0.7 | かなり正の相関がある |
| 0.7<r≦1 | 強い正の相関がある |
散布図
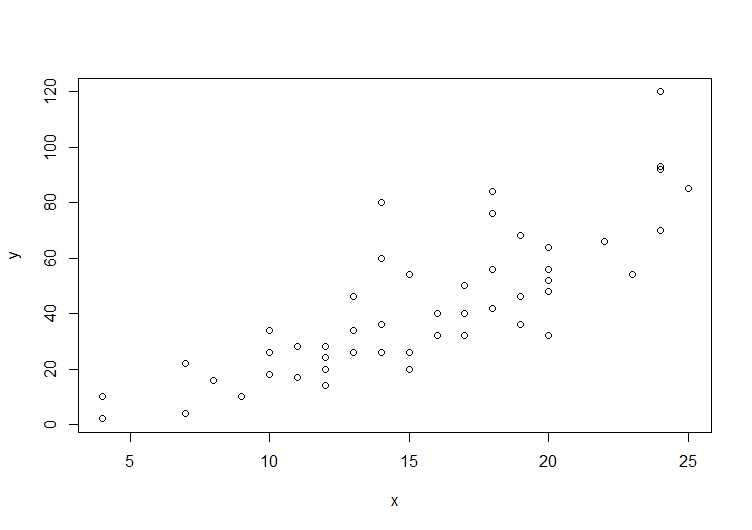
2変量のデータがあるときに、各要素(x,y)を座標の点としてグラフ化したものを散布図といいます。具体例は下のピアソンの積率相関係数の散布図を参照してください。
ピアソンの積率相関係数
一般的に、相関係数というときにはピアソンの積率相関係数を指すことが多いです。
統計Rに標準で含まれるサンプルデータcarsを用いて相関係数を計算してみます。carsは自動車の速度と停止までの時間をもつデータフレームです。
# 車の速度
x <- cars$speed
# 停止までの時間
y <- cars$dist
# 相関係数を計算(cor(x,y,method = "pearson")と同じ)
cor(x, y)
[1] 0.8068949
# 散布図を表示
plot(y ~ x)
スピアマンの順位相関係数
順位データから求める関係性の強弱を計る統計学的指標です。
x <- c(1, 2, 3, 4, 5)
y <- c(2, 4, 3, 5, 6)
cor(x, y, method = "spearman")
[1] 0.9
ケンドールの順位相関係数
順位データから求める関係性の強弱を計る統計学的指標です。
x <- c(1, 2, 3, 4, 5)
y <- c(2, 4, 3, 5, 6)
cor(x, y, method = "kendall")
[1] 0.8