ggplot2を用いて散布図と周辺分布をプロットする2つの方法をお伝えします。
最初の方法は、ggExtraパッケージのggMarginal関数を用いる方法で、周辺分布を簡単にプロットすることができます。
二番目の方法は、散布図と周辺分布を作成した上で、一つにまとめる方法です。
それぞれ一長一短があります。
最初の方法は、コード量が少ないですがグラフとしての見栄えや汎用性が二番目の方法よりは劣ります。
二番目の方法は、コード量が増えますがグラフとしての見栄えや汎用性が最初の方法よりは勝ります。
自分の確認用であれば最初の方法、他人がみる資料作成には二番目の方法を用いるなど、状況に応じて使い分ける必要があるかもしれません。
実際のコードとプロットされたグラフを合わせてご紹介します。
ggExtraパッケージを用いる方法
ggExtraパッケージのggMarginal関数を用いると、周辺分布を簡単にプロットできます。
ggMarginal関数の第一引数にはggplotオブジェクトを指定します。
また、type引数で周辺分布を「密度分布」「ヒストグラム」「箱ひげ図」「バイオリンプロット」として描くことを指定できます。
実際に、それぞの場合のコードとグラフを見ていきます。
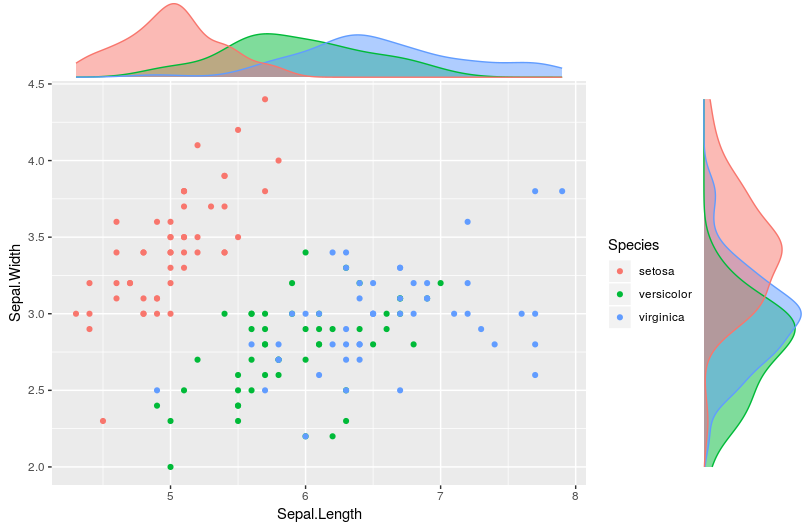
密度分布
library(ggplot2)
library(ggExtra)
data("iris")
g <- ggplot(iris, aes(x = Sepal.Length, y = Sepal.Width, colour = Species))
g <- g + geom_point()
ggMarginal(
g,
type = "density",
margins = "both",
size = 5,
groupColour = TRUE,
groupFill = TRUE
)
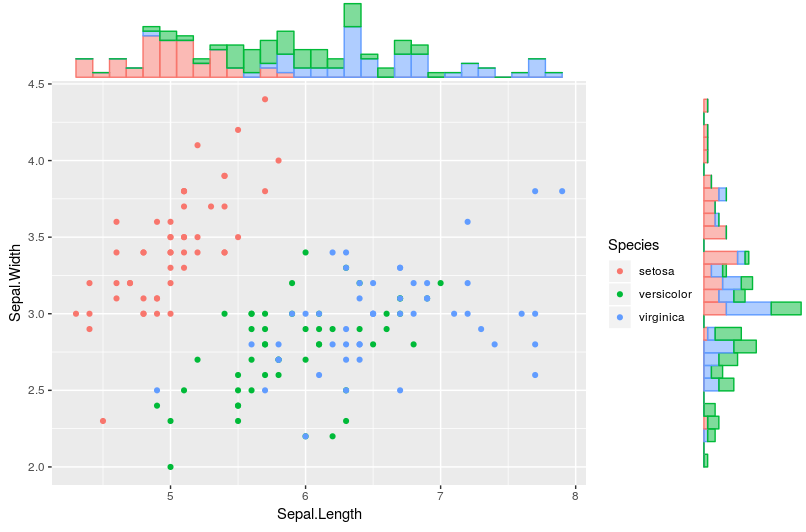
ヒストグラム
library(ggplot2)
library(ggExtra)
data("iris")
g <- ggplot(iris, aes(x = Sepal.Length, y = Sepal.Width, colour = Species))
g <- g + geom_point()
ggMarginal(
g,
type = "histogram",
margins = "both",
size = 5,
groupColour = TRUE,
groupFill = TRUE
)
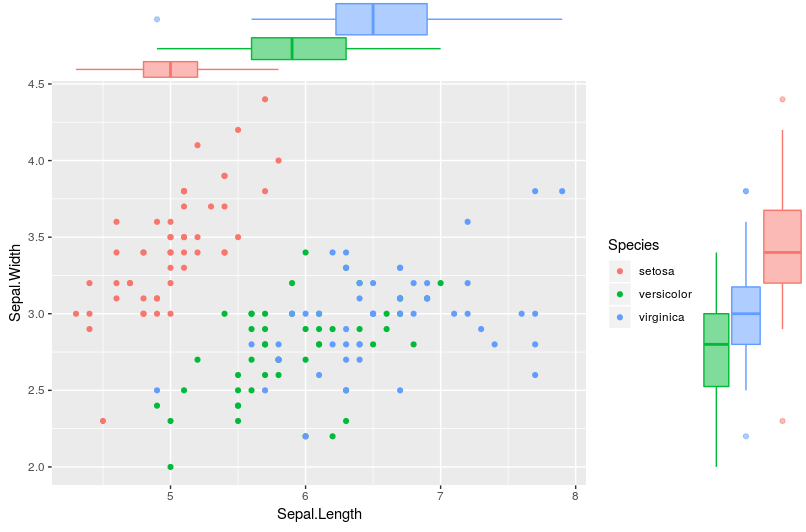
箱ひげ図
library(ggplot2)
library(ggExtra)
data("iris")
g <- ggplot(iris, aes(x = Sepal.Length, y = Sepal.Width, colour = Species))
g <- g + geom_point()
ggMarginal(
g,
type = "boxplot",
margins = "both",
size = 5,
groupColour = TRUE,
groupFill = TRUE
)
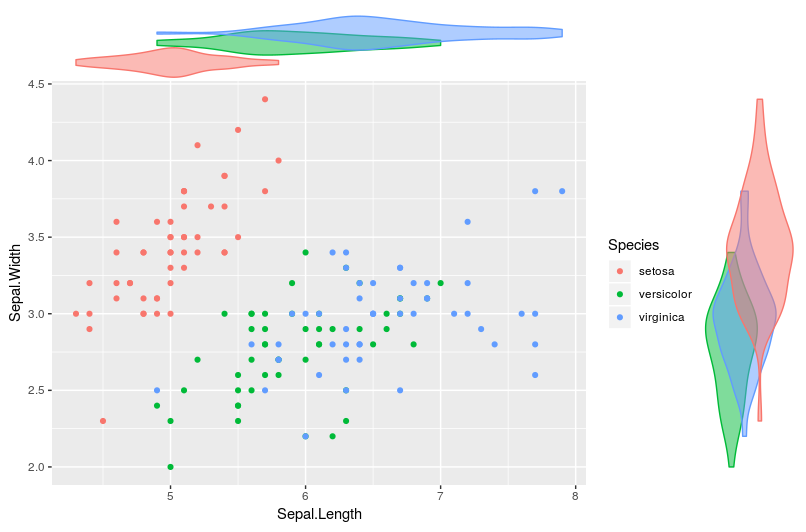
バイオリンプロット
library(ggplot2)
library(ggExtra)
data("iris")
g <- ggplot(iris, aes(x = Sepal.Length, y = Sepal.Width, colour = Species))
g <- g + geom_point()
ggMarginal(
g,
type = "violin",
margins = "both",
size = 5,
groupColour = TRUE,
groupFill = TRUE
)
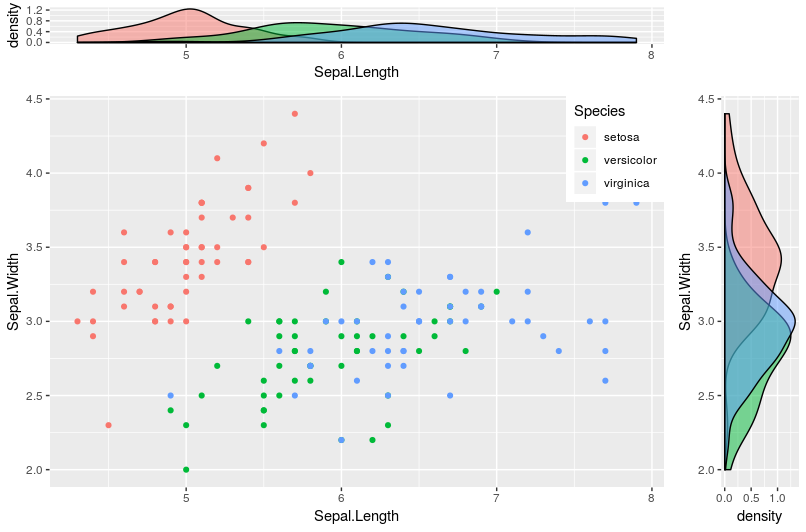
散布図と周辺分布を作成して一つにする方法
散布図と周辺分布を作成した上で、一つにまとめる方法をご紹介します。
それぞれを一つにまとめるには、gridExtraパッケージのgrid.arrange関数を用います。
grid.arrange関数は、グリッド状にggplotオプジェクトを配置することで一つのものとして取り扱います。
注意点としては、グリッド状に散布図と二つの周辺分布を配置したときには空欄用のggplotオブジェクトを指定しなければならないことです。
次のコードでは、panel.blankが空欄用に該当します。
library(ggplot2)
library(gridExtra)
data("iris")
panel.main <- ggplot(iris, aes(x = Sepal.Length, y = Sepal.Width, colour = Species))
panel.main <- panel.main + geom_point()
panel.main <- panel.main + theme(legend.position = c(1, 1),
legend.justification = c(1, 1))
panel.top <- ggplot(iris, aes(x = Sepal.Length, fill = Species))
panel.top <- panel.top + geom_density(alpha = 0.5)
panel.top <- panel.top + theme(legend.position = "none")
panel.right <- ggplot(iris, aes(x = Sepal.Width, fill = Species))
panel.right <- panel.right + geom_density(alpha = 0.5)
panel.right <- panel.right + coord_flip()
panel.right <- panel.right + theme(legend.position = "none")
panel.blank <- ggplot()
panel.blank <- panel.blank + geom_point(aes(1, 1), colour = "white")
panel.blank <- panel.blank + theme(plot.background = element_rect(colour = "white"),
panel.grid.major = element_blank(),
panel.grid.minor = element_blank(),
panel.border = element_blank(),
panel.background = element_blank(),
axis.title.x = element_blank(),
axis.title.y = element_blank(),
axis.text.x = element_blank(),
axis.text.y = element_blank(),
axis.ticks = element_blank())
grid.arrange(panel.top,
panel.blank,
panel.main,
panel.right,
ncol = 2,
nrow = 2,
widths = c(5, 1),
heights = c(1, 5))