R統計 度数分布表とヒストグラム

数値データの集合をただ眺めても、そのデータの特徴をつかむのは大変難しい。しかし、そのデータを表にまとめたもの、またはグラフにすると一目瞭然だ。特に、グラフにしたものは、大変分かりやすい。表にまとめたものを度数分布表、グラフにしたものをヒストグラムという。

では、早速具体的に見ていく。

度数分布表

度数分布表とは、以下の表のことを言う。ここで用いたデータは、統計Rに付属しているFisherの研究で使用されたirisデータを使用させていただいた。あやめ3品種のがく片の長さのデータである。

階級	階級値	度数	相対度数	累積度数	累積相対度数
4.0～4.2	4.1	0	0.000000000	0	0.000000000
4.2～4.4	4.3	4	0.026666667	4	0.026666667
4.4～4.6	4.5	5	0.033333333	9	0.060000000
4.6～4.8	4.7	7	0.046666667	16	0.010666667
4.8～5.0	4.9	16	0.106666667	32	0.213333333
5.0～5.2	5.1	13	0.086666667	45	0.300000000
5.2～5.4	5.3	7	0.046666667	52	0.346666667
5.4～5.6	5.5	13	0.086666667	65	0.433333333
5.6～5.8	5.7	15	0.100000000	80	0.533333333
5.8～6.0	5.9	9	0.060000000	89	0.593333333
6.0～6.2	6.1	10	0.066666667	99	0.660000000
6.2～6.4	6.3	16	0.106666667	115	0.766666667
6.4～6.6	6.5	7	0.046666667	122	0.813333333
6.6～6.8	6.7	11	0.073333333	133	0.886666667
6.8～7.0	6.9	5	0.033333333	138	0.920000000
7.0～7.2	7.1	4	0.026666667	142	0.946666667
7.2～7.4	7.3	2	0.013333333	144	0.960000000
7.4～7.6	7.5	1	0.006666667	145	0.966666667
7.6～7.8	7.7	4	0.026666667	149	0.993333333
7.8～8.0	7.9	1	0.006666667	150	1.000000000
合計		150	1.000000000

ここで、各言葉の意味は以下の通りである。

• 階級：データを分類するために分けた区分
• 階級値：各階級の中央値
• 度数：各階級内に含まれるデータの個数
• 相対度数：合計の度数の内、各階級の度数の割合
• 累積度数：階級の小さいほうから順に度数を累積した数値
• 累積相対度数：階級の小さいほうから順に相対度数を累積した数値

度数分布表

x <- iris$Sepal.Length
x1 <- table(cut(x,seq(4,8,0.2)))
# 累積度数
x2 <- cumsum(x1)
# 相対度数
x3 <- x1/150
# 累積相対度数
x4 <- x2/150
# まとめる
x5 <- cbind(x1,x2,x3,x4)
x5
          x1  x2          x3         x4
(4,4.2]    0   0 0.000000000 0.00000000
(4.2,4.4]  4   4 0.026666667 0.02666667
(4.4,4.6]  5   9 0.033333333 0.06000000
(4.6,4.8]  7  16 0.046666667 0.10666667
(4.8,5]   16  32 0.106666667 0.21333333
(5,5.2]   13  45 0.086666667 0.30000000
(5.2,5.4]  7  52 0.046666667 0.34666667
(5.4,5.6] 13  65 0.086666667 0.43333333
(5.6,5.8] 15  80 0.100000000 0.53333333
(5.8,6]    9  89 0.060000000 0.59333333
(6,6.2]   10  99 0.066666667 0.66000000
(6.2,6.4] 16 115 0.106666667 0.76666667
(6.4,6.6]  7 122 0.046666667 0.81333333
(6.6,6.8] 11 133 0.073333333 0.88666667
(6.8,7]    5 138 0.033333333 0.92000000
(7,7.2]    4 142 0.026666667 0.94666667
(7.2,7.4]  2 144 0.013333333 0.96000000
(7.4,7.6]  1 145 0.006666667 0.96666667
(7.6,7.8]  4 149 0.026666667 0.99333333
(7.8,8]    1 150 0.006666667 1.00000000

ヒストグラム

ヒストグラムとは、度数分布表をグラフに表したものである。以下のグラフは、上の度数分布表をグラフに表したものである。

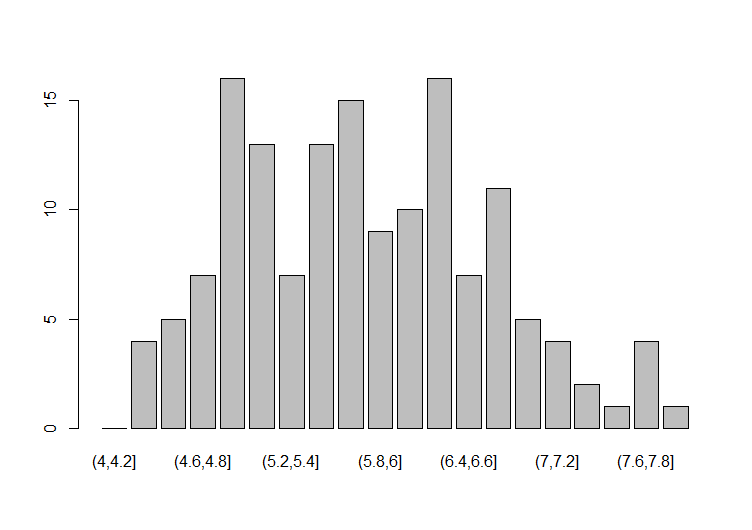
“(5.8,6]”の意味は、「5.8超6以下（5.8＜x≦6）」である。

ヒストグラム

x <- iris$Sepal.Length
hist(x)
# 階級を指定する場合
hist(x,breaks=seq(4,8,0.2))